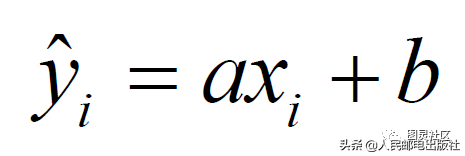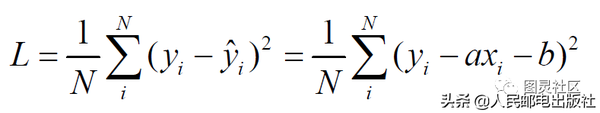题图来自Usplash

1 什么是PyTorch？

PyTorch是与TensorFlow、MXNet、Caffe等平行的深度学习开源框架。2017年初由Facebook首次推出，旨在实现快速，灵活的实验和高效生产。

PyTorch一经推出，便很快成为人工智能领域研究人员的热门选择。

在深度学习顶级会议ICLR的提交论文中，提及PyTorch的论文数从2017年的87篇激增到2018年的252篇，大有赶超深度学习框架佼佼者TensorFlow之势。

随着PyTorch 1.0的问世以及ONNX（Open Neural Network Exchange）深度学习开发生态的逐渐完备，PyTorch无疑成为众多深度学习框架中最值得期待的明日之星。

PyTorch为什么会这么受欢迎？

下面我们简单总结了4点原因。

1. 简单、易用、上手快

这一点对于初学者来说是极具吸引力的。

2. 功能强大

从计算机视觉、自然语言处理再到深度强化学习，PyTorch的功能异常强大。而且，如今支持PyTorch、功能强大的包也越来越多，例如Allen NLP和Pyro。

3. Python化编程

在诸多深度学习开源框架平台中，PyTorch恐怕是和Python结合得最好的一个。相比较TensorFlow框架来说，PyTorch将会让你的代码更流畅舒服。

4. 强大的社区支持

对于一个初学者来说，吸取到前辈的经验恐怕是最迫切的问题了。尽管PyTorch仅两岁有余，但是它的社区成长飞快。在国内，用PyTorch作为关键词搜索就能找到大概五六个网络社区、BBS。各大问答类网站关于PyTorch的问题数目也在持续增多。

PyTorch最大的特点就在于简单易用，特别适合新手快速掌握。

PyTorch与TensorFlow有什么区别？

到底哪个框架更适合学习？下面这篇知乎文章或许能帮到你：

《PyTorch还是TensorFlow？这有一份新手深度学习框架选择指南》

文中对这两个框架做了简单的对比，所以在这里我们就不再说了。PS：技术是发展的，文中的对比非绝对。

2 新手如何入门PyTorch？

其实PyTorch官网提供的的教程资源很全面，我们可以根据下面的步骤进行学习，此步骤来源知乎陈云的回答，原文地址：

https://www.zhihu.com/question/55720139/answer/147148105

1. PyTorch Tutorials > Deep Learning with PyTorch: A 60 Minute Blitz

60分钟入门，简单易懂。

https://pytorch.org/tutorials/

2. PyTorch Examples：

实现一个简单的例子，加深理解。

https://github.com/pytorch/examples

3. 通读PyTorch文档：

绝大部分文档都是作者亲自写的，质量很高。

https://pytorch.org/docs/stable/index.html

4. 论坛讨论：

论坛很活跃，没事刷一刷帖可以少走很多弯路。

https://discuss.pytorch.org/

5. 阅读源代码

通过阅读代码可以了解函数和类的机制，此外它的很多函数，模型,模块的实现方法都如教科书般经典。

其他：PyTorch资源合集：

https://github.com/ritchieng/the-incredible-pytorch

3 PyTorch示例：预测房价

下面我们引入一个实例问题：根据历史数据预测未来的房价。

我们将实现一个线性回归模型，并用梯度下降算法求解该模型，从而给出预测直线。

这个实例问题是：假如有历史房价数据，我们应如何预测未来某一天的房价？针对这个问题，我们的求解步骤包括：准备数据、模型设计、训练和预测。

一、准备数据

按理说，我们需要找到真实的房价数据来进行拟合和预测。简单起见，我们也可以人为编造一批数据，从而重点关注方法和流程。

首先，我们编造一批假的时间数据。假设我们每隔一个月能获得一次房价数据，那么时间数据就可以为0, 1, …，表示第0、1、2……个月份，我们可以由PyTorch的linspace来构造0~100之间的均匀数字作为时间变量x：

x = Variable(torch.linspace(0, 100).type(torch.FloatTensor))

然后，我们再来编造这些时间点上的历史房价数据。假设它就是在x 的基础上加上一定的噪声：

rand = Variable(torch.randn(100)) * 10
y = x   rand

这里的rand 是一个随机数，满足均值为0、方差为10 的正态分布。torch.randn(100)这个命令可以生成100个标准正态分布随机数（均值0，方差1）。于是，我们就编造好了历史房价数据：y。现在我们有了100 个时间点xi（i是下标）和每个时间点对应的房价yi（i是下标）。其中，每一个xi（i是下标）, yi（i是下标）称为一个样本点。

之后，我们将数据集切分成训练集和测试集两部分。所谓训练集是指训练一个模型的所有数据，所谓测试集则是指用于检验这个训练好的模型的所有数据。注意，在训练的过程中，模型不会接触到测试集的数据。因此，模型在测试集上运行的效果模拟了真实的房价预测环境。

在下面这段代码中，:-10 是指从x 变量中取出倒数第10 个元素之前的所有元素；而-10:是指取出x 中最后面的10 个元素。所以，我们就把第0 到90 个月的数据当作训练集，把后10 个月的数据当作测试集。

x_train = x[: -10]
x_test = x[-10 :]
y_train = y[: -10]
y_test = y[-10 :]

接下来，让我们对训练数据点进行可视化：

import matplotlib.pyplot as plt #导入画图的程序包

plt.figure(figsize=(10,8)) #设定绘制窗口大小为10*8 inch
#绘制数据，由于x 和y 都是Variable，需要用data 获取它们包裹的Tensor，并转成Numpy
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'o')
plt.xlabel('X') #添加X 轴的标注
plt.ylabel('Y') #添加Y 轴的标注
plt.show() #画出图形

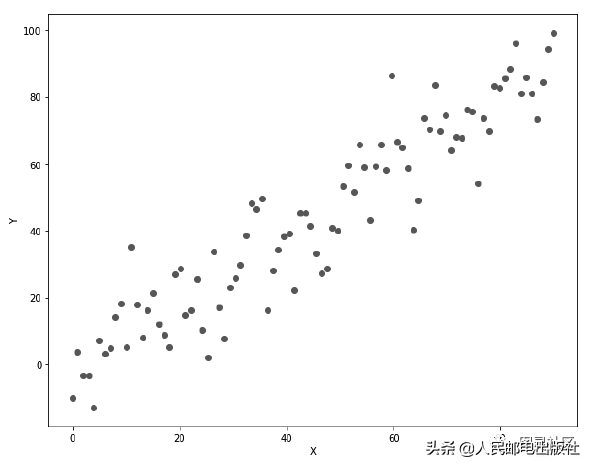
最终得到的输出图像如图1所示。

图1 人造房价数据的散点图

通过观察散点图，可以看出走势呈线性，所以可以用线性回归来进行拟合。

二、模型设计

我们希望得到一条尽可能从中间穿越这些数据散点的拟合直线。设这条直线方程为：

y=ax b

接下来的问题是，求解出参数a、b 的数值。我们可以将每一个数据点xi（i下标）代入这个方程中，计算出一个ˆyi（i下标），即：

显然，这个点越靠近yi（i下标）越好。所以，我们只需要定义一个平均损失函数：

并让它尽可能地小。其中N 为所有数据点的个数，也就是100。由于xi（i下标）, yi （i下标）都是固定的数，而只有a 和b 是变量，那么L 本质上就是a 和b 的函数。所以，我们要寻找最优的a、b 组合，让L 最小化。

我们可以利用梯度下降法来反复迭代a 和b，从而让L 越变越小。梯度下降法是一种常用的数值求解函数最小值的基本方法，它的基本思想就像是盲人下山。这里要优化的损失函数L(a, b)就是那座山。假设有一个盲人站在山上的某个随机初始点（这就对应了a 和b 的初始随机值），他会在原地转一圈，寻找下降最快的方向来行进。所谓下降的快慢，其实就是L 对a、b 在这一点的梯度（导数）；所谓的行进，就是更新a 和b 的值，让盲人移动到一个新的点。于是，每到一个新的点，盲人就会依照同样的方法行进，最终停留在让L 最小的那个点。

我们可以通过下面的迭代计算来实现盲人下山的过程：

α 为一个参数，叫作学习率，它可以调节更新的快慢，相当于盲人每一步的步伐有多大。α 越大，a、b 更新得越快，但是计算得到的最优值L 就有可能越不准。

在计算的过程中，我们需要计算出L 对a、b 的偏导数，利用PyTorch 的backward()可以非常方便地将这两个偏导数计算出来。于是，我们只需要一步一步地更新a 和b 的数值就可以了。当达到一定的迭代步数之后，最终的a 和b 的数值就是我们想要的最优数值，y=ax b 这条直线就是我们希望寻找的尽可能拟合所有数据点的直线。

三、训练

接下来，就让我们将上述思路转化为PyTorch 代码。首先，我们需要定义两个自动微分变量a 和b：

a = Variable(torch.rand(1), requires_grad = True)
b = Variable(torch.rand(1), requires_grad = True)

可以看到，在初始的时候，a 和b 都是随机取值的。设置学习率：

learning_rate = 0.0001

然后，完成对a 和b 的迭代计算：

for i in range(1000):
#计算在当前a、b 条件下的模型预测数值
predictions = a.expand_as(x_train) * x_train   b.expand_as(x_train)
loss = torch.mean((predictions - y_train) ** 2) #通过与标签数据y 比较，计算误差
 print('loss:', loss)
 loss.backward() #对损失函数进行梯度反传
 #利用上一步计算中得到的a 的梯度信息更新a 中的data 数值
 a.data.add_(- learning_rate * a.grad.data)
 #利用上一步计算中得到的b 的梯度信息更新b 中的data 数值
 b.data.add_(- learning_rate * b.grad.data)#增加这部分代码，清空存储在变量a、b 中的梯度信息，以免在backward 的过程中反复不停地累加
 a.grad.data.zero_() #清空a 的梯度数值
 b.grad.data.zero_() #清空b 的梯度数值

这个迭代计算了1000 步，当然我们可以调节数值。数值越大，迭代时间越长，最终计算得到的a、b 就会越准确。在每一步迭代中，我们首先要计算predictions，即所有点的ˆyi ；然后计算平均误差函数loss，即前面定义的L；接着调用了backward()函数，求L 对所有计算图中的叶节点（a、b）的导数。于是，这些导数信息分别存储在了a.grad 以及b.grad 之中；然后，通过a.data.add_(-learning_rate * a.grad.data)完成对a 数值的更新，也就是a 的数值应该加上一个-learning_rate 乘以刚刚计算得到的L 对a 的偏导数值，b 也进行同样的处理；最后，在更新完a、b 的数值后，需要清空a 中的梯度信息（a.grad.data.zero_()），否则它会在下一步迭代的时候自动累加。于是，一步迭代完成。

整个计算过程其实是利用自动微分变量 a 和b 来完成动态计算图的构建，然后在其上进行梯度反传的过程。所以，整个计算过程就是在训练一个广义的神经网络，a 和b 就是神经网络的参数，一次迭代就是一次训练。

另外，有以下几点技术细节值得说明。

• 在计算predictions 时，为了让a、b 与x 的维度相匹配，我们对a 和b 进行了扩维。我们知道，x_train 的尺寸是(90, 1)，而a、b 的尺寸都是1，它们并不匹配。我们可以通过使用expand_as 提升a、b 的尺寸，与x_train 一致。a.expand_as(x_train)的作用是将a的维度调整为和x_train 一致，所以函数的结果是得到一个尺寸为(90, 1)的张量，数值全为a 的数值。
• 不能直接对一个自动微分变量进行数值更新，只能对它的data 属性进行更新。所以在更新a 的时候，我们是在更新a.data，也就是a 所包裹的张量。
• 在PyTorch中，如果某个函数后面加上了“_”，就表明要用这个函数的计算结果更新当前的变量。例如，a.data.add_(3)的作用是将a.data 的数值更新为a.data 加上3。

最后，将原始的数据散点联合拟合的直线通过图形画出来，如下所示：

x_data = x_train.data.numpy() #将x 中的数据转换成NumPy 数组
plt.figure(figsize = (10, 7)) #定义绘图窗口
xplot, = plt.plot(x_data, y_train.data.numpy(), 'o') #绘制x, y 散点图
yplot, = plt.plot(x_data, a.data.numpy() * x_data  b.data.numpy()) #绘制拟合直线图
plt.xlabel('X') #给横坐标轴加标注
plt.ylabel('Y') #给纵坐标轴加标注
str1 = str(a.data.numpy()[0])   'x  '   str(b.data.numpy()[0]) #将拟合直线的参数a、b 显示出来
plt.legend([xplot, yplot],['Data', str1]) #绘制图例
plt.show() #将图形画出来

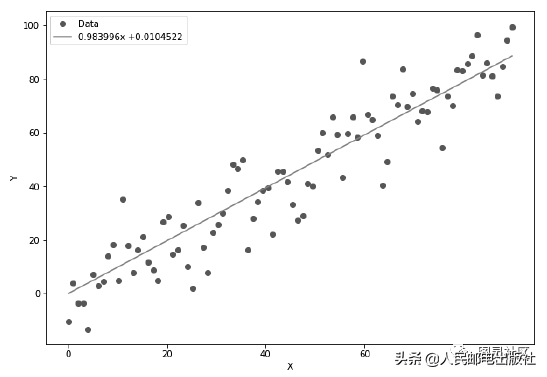
最后得到的图像如图2所示：

图2 数据点与拟合曲线

看来我们得到的拟合结果还不错。

四、预测

最后一步就是进行预测。在测试数据集上应用我们的拟合直线来预测出对应的y，也就是房价。只需要将测试数据的x 值带入我们拟合好的直线即可：

predictions = a.expand_as(x_test) * x_test   b.expand_as(x_test) #计算模型的预测结果
predictions #输出

最终输出的预测结果为：

Variable containing:
89.4647
90.4586
91.4525
92.4465
93.4404
94.4343
95.4283
96.4222
97.4162
98.4101
[torch.FloatTensor of size 10]

那么，预测的结果到底准不准呢？我们不妨把预测数值和实际数值绘制在一起，如下所示：

x_data = x_train.data.numpy() #获得x 包裹的数据
x_pred = x_test.data.numpy() #获得包裹的测试数据的自变量
plt.figure(figsize = (10, 7)) #设定绘图窗口大小
plt.plot(x_data, y_train.data.numpy(), 'o') #绘制训练数据
plt.plot(x_pred, y_test.data.numpy(), 's') #绘制测试数据
x_data = np.r_[x_data, x_test.data.numpy()]
plt.plot(x_data, a.data.numpy() * x_data   b.data.numpy()) #绘制拟合数据
plt.plot(x_pred, a.data.numpy() * x_pred   b.data.numpy(), 'o') #绘制预测数据
plt.xlabel('X') #更改横坐标轴标注
plt.ylabel('Y') #更改纵坐标轴标注
str1 = str(a.data.numpy()[0])   'x  '   str(b.data.numpy()[0]) #图例信息
plt.legend([xplot, yplot],['Data', str1]) #绘制图例
plt.show()

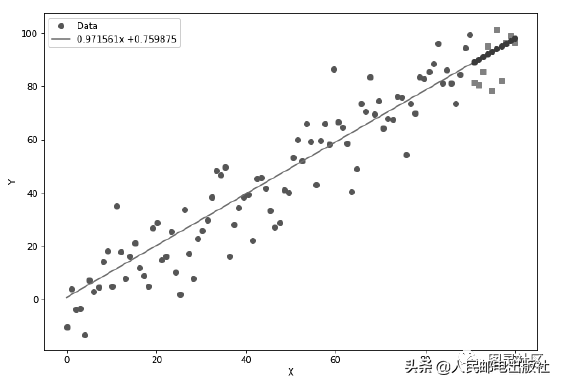
最终得到的图像如图3 所示：

图3 拟合曲线及其预测数据

图中的方块点表示测试集中实际的房价数据，直线上的圆点则表示在测试集上预测的房价数据。我们还可以计算测试集上的损失函数，来检验模型预测的效果，在此不再赘述。

——示例内容节选自《深度学习原理与PyTorch实战》

10个PyTorch实战案例

10个实战示例来源于《深度学习原理与PyTorch实战》，这是一本系统介绍PyTorch的入门书。全书共12章，前2章是深度学习和PyTorch简介，后面10章，每章一个实战示例。

深度学习原理与PyTorch实战

1. 单车预测器——你的第一个神经网络
2. 机器也懂感情——中文情绪分类器
3. 手写数字识别器——卷积神经网络
4. 写数字加法机——迁移学习
5. 自己的Prisma——图像风格迁移
6. 人工智能造假术——图像生成与对抗学习
7. 词汇的星空——词向量与Word2Vec
8. LSTM作曲机——序列生成模型
9. 神经翻译机——端到端的机器翻译模型
10. AI游戏高手——深度强化学习

读完这本书，我们可以轻松入门深度学习，学会构造一个图像识别器，生成逼真的图画，让机器理解单词与文本，让机器作曲，教会机器玩游戏，还可以实现一个简单的机器翻译系统等。

深度学习原理与PyTorch实战

——

集智俱乐部 著

—— 集智俱乐部 ——

诞生于2003年，是国内最早的人工智能社区之一。经过十几年的发展，已经逐渐成长为一个深受国内顶尖研究者、科学家、工程师和学生群体热爱的学术社区。

在这十几年间，集智俱乐部举办了大大小小400多场讲座、读书会等活动，创作了《科学的极致：漫谈人工智能》和《走近2050：注意力、互联网与人工智能》两本人工智能科普读物。

值得一提的是，国内AI领域著名的创业黑马“Momenta”和“彩云AI”的创始人及核心成员都来自于集智俱乐部。

全书注重实战，每章围绕一个有意思的实战案例展开，不仅循序渐进地讲解了PyTorch的基本使用、神经网络的搭建、卷积神经网络和循环神经网络的实现，而且全面深入地介绍了计算机视觉、自然语言处理、迁移学习，以及最新的对抗学习和深度强化学习等前沿技术。

本书资源

本书配有源代码、习题和视频课程，让你轻松入门深度学习，快速上手PyTorch。