本期笔记内容综述

Python函数定义再回顾
函数的参数传递
Python函数递归问题

7分钟学习系列

1.Python函数再回顾

著名的斐波拉契数列
除了第一个数和第二个数外，任意一个数都可由前两个数相加得到：1，1，2，3，5，13，21，34····

且先看看定义

F1=1 F2=1
将上面文字转化为符号语言:Fn=Fn-1 Fn-2 n>2
由于Python索引号从0开始，因此我们把开始改为0.
代码运行[1]

且先看看前几项

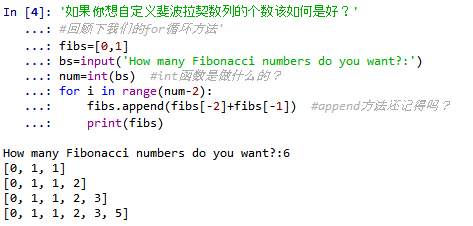
问题:如果你想自定义斐波拉契数列的个数该如何是好？'
代码运行[2]

for 循环

'函数该如何写呢？'

函数结果

问题：如果只要展示指定的斐波拉契数列数呢？

运行结果

'range()函数再介绍'

range(i,j，[步长值])，默认步长为1,创建的对象表示值为i到j-1的整数。

rang( )函数

2.Python函数的参数传递

从一个栗子开始：

梯形面积：Trapezoid area
我们来设计一个名为：Trapezoid_area的函数计算梯形的面积
三个参数分别为：base_up（上底），base_down（下底），height（高）
梯形的面积=(上底下底)×高÷2

代码运行

运行结果

'不难看出来参数1，2，3分别对应base_up（上底），base_down（下底），height（高）。

提供关键字参数传导

关键字参数传导如何调用呢？
方法：在调用函数名后面圆括号内（参数关键字2=参数值，参数关键字1=参数值），不必拘泥于原来的顺序了。
代码运行[1]

代码运行结果

代码运行结果[2]

结果2

'调用函数提供参数的时候，按顺序传递的参数是要位于关键字参数之前，而且不能有重复的情况'

3.Python函数递归问题

重大问题：递归
我想递归这个词大家最初接触的时候是曾经了解数列的时候，
其实我们之前给出的斐波拉契数列就是一个递归，可以无穷的进行下去。
接下来我们再看两个常见的递归：阶乘和幂

3.1阶乘

且先看排列

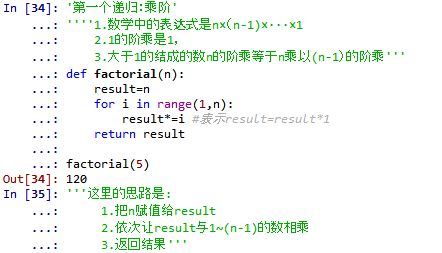
且看栗子：

代码1

递归写法

递归结果

3.2 幂

基础函数写法

'更改为递归模式:'
1.对于任意数字x来说,power(x,0)结果是1，任何数的零次幂都是1
2.对于任何大于0的数来说，power(x,n)是x乘以power(x,n-1)
其实写递归首先要做的是理解概念

递归结果

'可是我还是没看出递归到底和循环的帮助有多大？'
'还记得昨天的课后题吗？'

上一期笔记内容问题解答

回顾问题

问题回顾

'现在来看看当初绞尽脑汁写的上面这串代码吧，来思考下如何写它的递归'

'''首先我们来总结下前面两个的递归的例子的方法:

1.核心：找到一个初始值，再找到一个递归循环部分；

2.初始值：最外层没进行的递归部分的最开始的基本实例反应值；{递归一定要有函数返回值，否者就永不停止了}

3.递归部分：找到重复出现的部分，如前两个栗子中相邻两个的关系：第n个和第n-1的结果的关系即递推式.

4.用条件语句中一个分支写初始值的，一部分写递归循环部分调用自身的函数。

5.关键：理解定所要做的事情的含义。#其实可以参考数学归纳法来理解

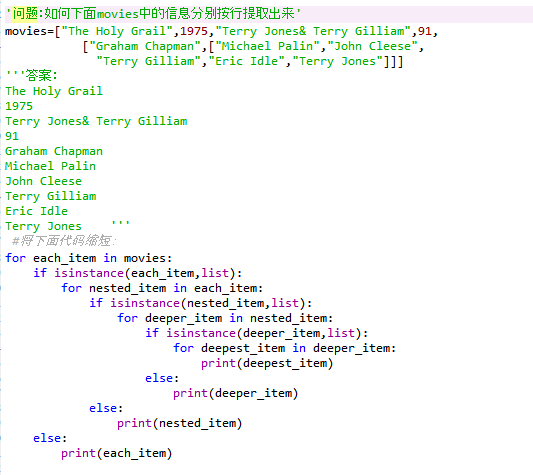
isinstance( )函数是检查某个特定的标识符是否含有某个数据类型，在这里之所以写出上面如此复杂的函数：是因为单独的一个for循环下来，列表中的列表是全部打印出来，而不能全部按行提取出来
重新观看代码，很快我们发现：

代码问题

1.上面代码12行和34，56，7行基本一致，只是换了个元素名和列表名在重复。从这里我们可以找递归循环体

2.根据意图可知：都在做一件事情，判断元素是否属于列表，如果不是就输出元素（初始对应值），如果是继续操作下去（递归循环体部分）。

3.代码运行:

问题答案

对比下两段代码，我相信你一定体会到递归的方便的吧。
程序员在解决问题位目标的基础下，应该学会偷懒。
不管影迷的信息需要多少更深层的嵌套列表，递归函数不需要做任何改变可以任意处理。

3.3 二分法原理

要求：必须掌握,请自己编写一个二分法的操作，不要局限于下面代码。
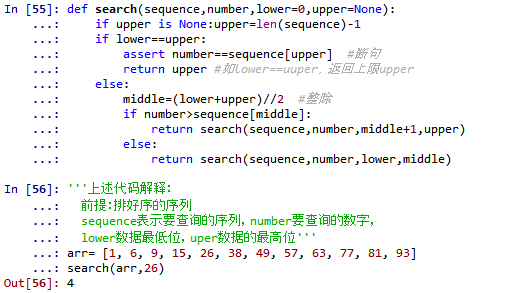
'''首先什么是二分法呢？先看看定义确保自己知道接下来在做什么。

前提：排好序
若上下限相同，则那就是数字所在位置，返回；
否则，找到两者的中间，查找数字是在左侧还是右侧，继续查找数字所在的那半部分。

在给出的有序排列的数组中，把目标值和数组中间值进行比较，

1.如果相等，则返回中间值下标，

2.如果目标值小于中间值，就从数组的前半段（左侧）再次执行二分法查找，

3.如果目标值大于中间值，从数组的后半段（右侧）开始二分法查找。

代码运行

二分法

很抱歉，似乎内容已经超过7分钟来理解了。
好了，本期笔记分享内容就到此以歉意结束，茄子暂别，每天都美好。祝愿生活愉快！

python递归函数例题（Python递归函数）